Do you have students who struggle with simplifying fractions and need an alternate approach? It happens to me every year. No matter how hard I try to teach using traditional methods, some kids just don’t get it. Luckily, the ladder method is just what some kids need.
Before we get our hands dirty, a little context: the ladder method might remind your students of a layered cake. Because of this, many people refer to this as the cake method. But instead of candles and frosting, we’re working with numbers. Yummy, right?
Why Use the Ladder Method?
Here’s the scoop on why this method is a game-changer:
Visual Representation: Many students are visual learners. With this method, kids can literally see how numbers break down and relate to each other.
Systematic Approach: It’s like following a recipe. Step by step, no chaos.
Building Number Sense: It’s like flexing those math muscles. The more kids work with factors and multiples, the stronger their number sense gets.
Flexibility: The ladder method can be used in a variety of ways. It can be used to find the greatest common factor, the least common multiple, and to simplify fractions.
Mastering the Ladder Method in a Few Simple Steps
Here’s how the ladder method works:
1. Write the numbers: Write the numerator and the denominator side by side.
2. Draw a cake layer: Draw an “L” or a cake layer underneath the numbers.
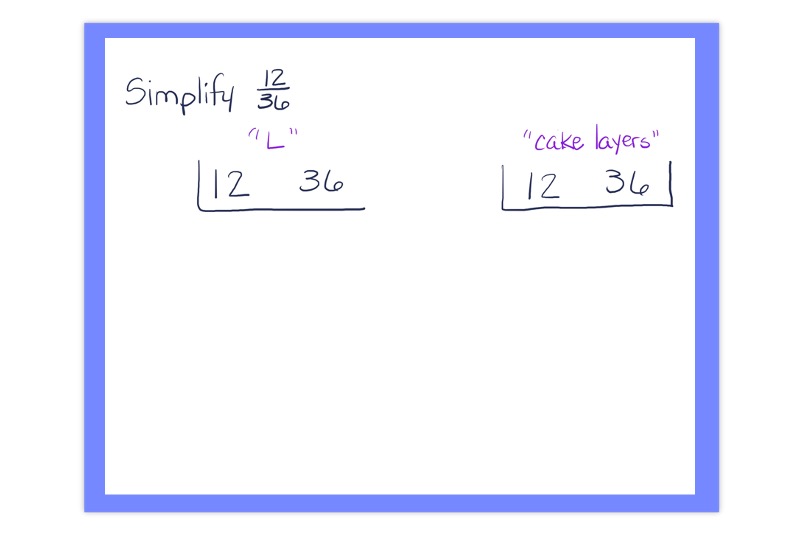
3. Find a Common Factor: Do a little detective work and find a number that both numbers can be divided by. The great thing about this method is that any factor will do. Students don’t have to worry about finding the largest common factor.
4. Write the Factor: Write the chosen factor to the left of the “L” or cake layer.
5. Divide: Divide both numbers by the factor and write the quotients underneath.
6. Repeat: Draw another “L” or cake layer and repeat the process until the quotients are both prime.
7. Voilà, Your Simplified Fraction!: The remaining quotients are the numerator and denominator of your simplified fraction.

Considerations
Students’ work may look different when using the ladder method (cake method). For instance, when simplifying 36/48, one student may recognize that the numerator and denominator are divisible by 12, while another student may start by dividing both by 2.

Finding the GCF with the Ladder Method
If you want your students to find the greatest common factor using this method, all they have to do is look at the numbers to the left of the cake once all the layers have been completed. Multiply these numbers together to get the GCF.
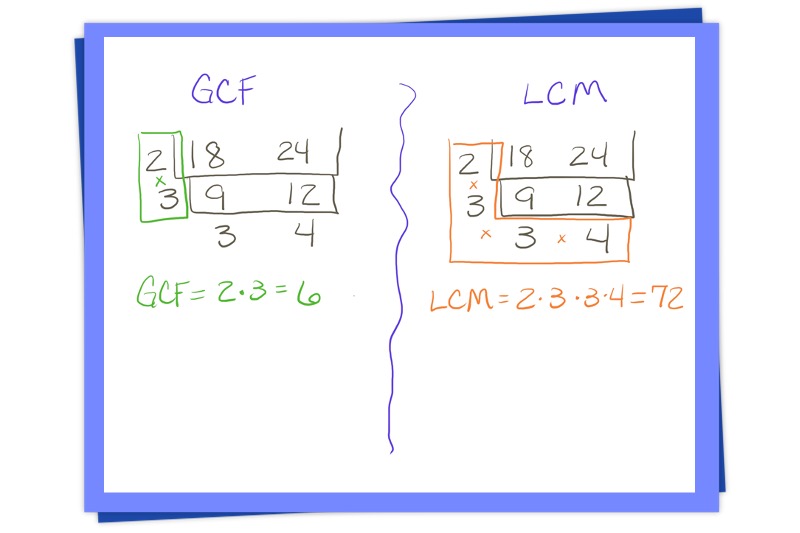
Finding the LCM
Students can find the least common multiple of the two numbers by drawing an “L” around the numbers on the outside of the cake. Then, multiply all these numbers together to get the LCM.
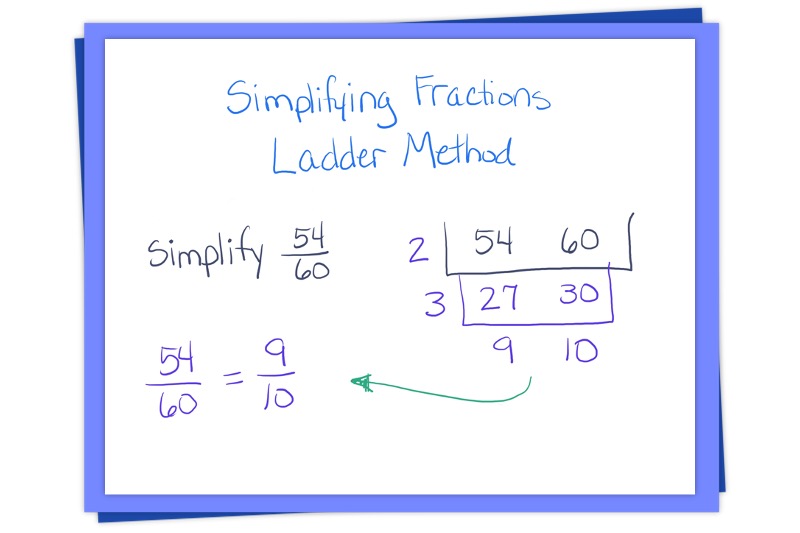
Simplifying Fractions with the Ladder Method
Simplifying fractions doesn’t have to be as hard as resisting a slice of chocolate cake. With the ladder method in your arsenal, it might even be—dare I say—fun? Not only can your students simplify fractions with this method, but they can also find the GCF and LCM. So give it a whirl, adapt as you see fit, and make math a piece of cake!
Looking for Ladder Method Practice?
Check out these simplifying fractions worksheets that provide scaffolded practice for your students. This resource of 29 worksheets includes pages designed around the ladder method.
















